Regulatory PID na Arduino. Wstęp
W tym tekście postaram się przybliżyć ideę regulatorów PID, ich zastosowania oraz sposób implementacji w języku C. Jest to wstęp do cyklu wpisów o regulatorach w robotyce. W tej serii nie będę się zagłębiał w Teorię Sterowania, zamiast tego skupię się na wykorzystaniu omówionych regulatorów w praktyce.
Czym to się je, czyli co to jest regulator
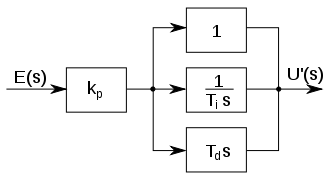
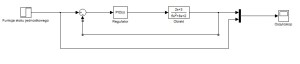
W Teorii Sterowania istnieje pojęcie układu regulacji automatycznej (URA). Schemat blokowy takiego układu wygląda tak:
Sygnał zadany to np. napięcie zasilania silnika elektrycznego lub serwa. Analogicznie może być to zasilanie pompy wodnej, dopływ paliwa do silnika spalinowego itp. Obiekt to rzecz, która ma być kontrolowana np. silnik. Sygnał wyjściowy to np. prędkość obrotowa wału silnika. Dodanie regulatora i sprzężenia zwrotnego ma celu stworzenie sytuacji, w której mimo pojawienia się zakłóceń (np. zmiana obciążenia silnika) układ sam będzie wracał do stanu określonego przez sygnał zadany. Ot cała filozofia ;)
Nazwa regulatora PID pochodzi od nazw jego poszczególnych członów:
- Proporcjonalnego (P – proportional)
- Całkującego (I – integral)
- Różniczkującego (D – derivative)
Każdy z członów może z powodzeniem występować sam jako regulator lub w innej kombinacji, stąd powszechne występowanie regulatorów P, PI, PD. Regulator na wyjściu daje nam „u” czyli tzw. sygnał sterujący, a pracuje na uchybie „e” – czyli różnicy aktualnej wartości sygnału od wartości zadanej. Żeby nie zagłębiać się w teorię nie będę podawał wzorów opisujących regulator PID ;) Postaram się wytłumaczyć to intuicyjnie. Wystarczy pamiętać, że są cztery istotne wielkości: „Kp”, „Ki”, „Kd” – czyli wzmocnienia poszczególnych części regulatora oraz „dt”, czyli co jaki czas pobiera się próbkę. Możecie się też spotkać z innymi parametrami opisującymi regulator, np na Wikipedii, czyli „Ti” i „Td”. „Ki” to iloraz „Kp” i „Ti” pomnożony przez „dt”, a „Kd” to iloczyn „Kp” i „Td” podzielony przez „dt” :) Opis jest długi, ale te parametry stosuje się wymiennie, w zależności od potrzeb. Tak samo jak rezystancję i konduktancję czy impedancję i admitancję, stosuje się je wymiennie dla wygody – by zastąpić dzielenia mnożeniami.
Działanie regulatora PID postaram się zaprezentować przy pomocy kilku charakterystyk przedstawiających zmianę regulowanej wartości w czasie. Są to tzw. odpowiedzi skokowe, ponieważ na wejście regulatora podajemy skok od 0 do 1 (fioletowy wykres), a na wyjściu dostajemy coś… innego. Zadanie regulatora jest proste: sprawić, by to co było na wyjściu było takie samo jak na wejściu.

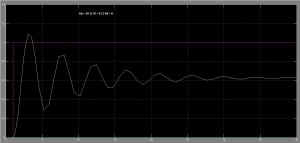
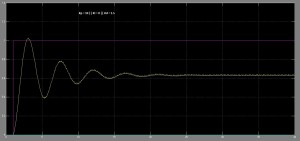
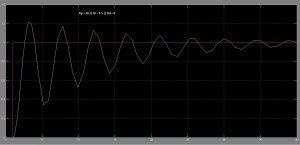
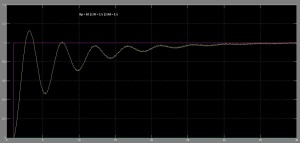
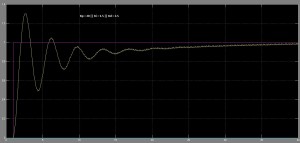
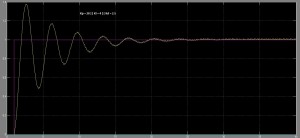
Jak widać, zależnie od wartości Kp , Ki oraz Kd zmienia się charakterystyka sygnału wyjściowego. Został zadany sygnał o wartości 1, cała rzecz polega na tym by jak najszybciej na wyjściu też dostać 1. Bez żadnego regulatora, bez sprzężenia, sygnał stabilizował się na poziomie 0.25 – to za mało. Wzmocnienie członu proporcjonalnego zwiększa siłę sygnału wyjściowego i przyspiesza osiąganie wartości zadanej, a człon całkujący pozwala na pozbycie się uchybu całkowitego (wartość sygnału w nieskończoności osiąga wartość zadaną, błąd wynosi zero). Stąd przy wysokiej wartości Ki sygnał pod koniec czasu trwania symulacji był dosyć blisko wartości zadanej. Zadałem zbyt dużą wartość Kd i dlatego pojawiły się zniekształcenia. Niemniej, znacznie przyspieszył osiągnięcie wartości zadanej. Podsumowując, człon P regulatora odpowiada za korektę błędu z teraźniejszości, człon I – błędu z przeszłości, a człon D stara się pozbyć błędu jaki będzie w przyszłości.
Regulatory PID – zastosowanie
W zależności od zastosowania wykorzystuje się różne regulatory. Człon całkujący jest bardzo wolny, nie przydaje się tam gdzie coś się szybko zmienia. Dlatego regulatory PI i PID znajdują zastosowanie przy regulacji temperatury, przy trymowaniu pracy pompy ciepła, itp. Mają one na tyle dużą inercję, że mała szybkość reakcji członu całkującego nie jest problemem, a pozwala cieszyć się ze swojej właściwości – likwidowania uchybu do zera. W ten sposób, po ustawieniu termostatu na 20 stopni, po pewnym czasie faktycznie w pokoju jest 20 stopni, nie mniej i nie więcej. Prędkość robota zmienia się dosyć szybko, w związku z tym w robotyce stosuje się głównie regulatory PD. Oczywiście regulatory P, PI, PD i PID to nie jedyne rodzaje regulatorów, są jeszcze regulatory histerezowe, dwupołożeniowe, step-forward i wiele, wiele więcej.
Implementacja
Wzór opisujący mechanikę regulatora PID, opisany wyżej, należy teraz przedstawić w sposób zjadliwy dla Arduino. Cytując Abrahama Lincolna: „Każda praca jest możliwa do wykonania jeśli podzielić ją na małe odcinki.”. Zgodnie z opisem wyżej, regulator ma trzy niezależne człony, rozdzielmy je zatem. Zacznijmy od najtrudniejszego – członu całkującego.
Trzeba zaimplementować w programie całkę. Co to jest całka? Jest to suma nieskończenie wielu, nieskończenie małych fragmentów. Intuicyjnie, całkę oznaczoną można rozumieć jako pole między wykresem funkcji f(x) a osią x. Funkcją f(x) może być np. zmiana temperatury czy prędkości w czasie, zmiana wychylenia w funkcji położenia, etc. Właśnie to pole pod wykresem trzeba policzyć. Jest wiele metod numerycznych, opracowanych przez ludzi znacznie mądrzejszych niż ja, do liczenia wartości całek funkcji. Każda metoda niesie ze sobą pewien błąd, niestety – z reguły im metoda jest prostsza tym błąd jest większy. Najpopularniejsze w prostych zastosowaniach, gdzie taki błąd można tolerować, jest całkowanie metodą prostokątów i trapezów.
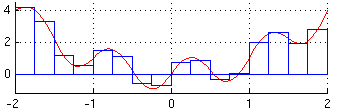
Metoda prostokątów
Zgodnie z rysunkiem, pole pod wykresem dzieli się na prostokąty.
Powstające po połączeniu „ząbki” to błąd tej metody. Pole pod wykresem funkcji można policzyć sumując pola wszystkich prostokątów. Szerokością prostokąta jest malutki fragment osi rzędnych, z kolei wysokością – wartość funkcji, np. temperatura wody w danej chwili. Zmniejszając szerokość „fragmentu” na osi czasu, zwiększa się gęstość próbkowania co poprawia dokładność całkowania.
int dt = 20; //podstawa prostokąta, co ile pobiera się próbkę int e; //uchyb int y; //wynik całkowania
...
void loop()
{
e = analogRead(2); //tutaj założyłem, że wartość uchybu poznajemy za pomocą odczytu z pinu A2
y += e*dt;
}
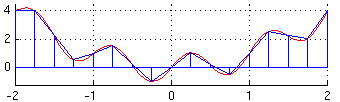
Metoda trapezów jest analogiczna do metody prostokątów, z tą różnicą, że zamiast liczenia pól prostokątów – oblicza się pola trapezów.
int dt = 20; //co ile pobiera się próbkę int ep; //uchyb poprzedni int en; //uchyb następny int y; //wynik całkowania
...
void loop()
{
en = analogRead(2); //tutaj założyłem, że wartość uchybu poznajemy za pomocą odczytu z pinu A2
y += ((ep + en)/2)*dt;
ep = en;
}
Człon różniczkujący
Opis wzorem różniczki wygląda następująco:
gdzie f’(x) to pochodna opisana wzorem:
Te dwa dziwne wzory najprościej można wytłumaczyć tak: różniczka to nieskończenie mała zmiana danej zmiennej. Taka jakby mała różnica ;) Dlatego można pokusić się o taki zapis:
Pod warunkiem, że nie dzieli tych kolejnych wartości duża odległość wzdłuż osi x.
int dt = 20; //co ile pobiera się próbkę int ep; //uchyb poprzedni int en; //uchyb następny int y; //różniczka
...
void loop()
{
en = analogRead(2); //tutaj założyłem, że wartość uchybu poznajemy za pomocą odczytu z pinu A2
y = (en - ep)/dt;
ep = en;
}
Nadszedł czas by zebrać wszystko w całość.
int dt = 20; //co ile pobiera się próbkę int ep; //uchyb poprzedni int en; //uchyb następny int U; //sygnał sterujący int C; //część całkująca int Kp; //wzmocnienie int Ti; //stała całkowania int Td; //stała różniczkowania
...
void loop()
{
en = analogRead(2); //tutaj założyłem, że wartość uchybu poznajemy za pomocą odczytu z pinu A2
C += ((ep + en)/2)*dt;
U = Kp*(en + (1/Ti)*C/1000 + Td*(en - ep)*1000/dt)
ep = en;
}
Skąd się wzięło to mnożenie i dzielenie przez 1000? Chodzi o zamianę jednostek na jednostki SI, z milisekund na sekundy. Kod wycinałem z pewnego projektu nad którym ugrzęzłem i ta zamiana to pozostałość po nim.
W następnym artykule postaram się omówić różne metody doboru nastaw regulatora, a trzeba przyznać, że nie jest to rzecz lekka ;) Ale warta zachodu, gdyż dobrze ustawiony regulator potrafi zdziałać cuda.
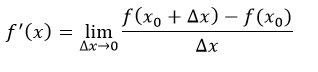

Super sprawa. Kiedyś interesowałem się tym tematem, ale sam bym tego lepiej nie opisał.
Dzięki ;)
Schemat blokowy jest niepoprawny. Regulator powinien byc zaraz za sprzężeniem, dopiero potem obiekt. Matematycznie to nie ma znaczenia, ale praktycznie juz tak. W tekście opisana jest juz wlasciwa kolejność.
Jeszcze jedna uwaga, element rozniczkujacy w układach cyfrowych zwykle liczy się z więcej niż dwóch kolejnych chwil czasowych, a całce trzeba dać ograniczenie, gdyż dosyć szybko przepelni pamięć.
Dzięki, nie zauważyłem tego.
Masz rację, chciałem tutaj opisać ogólną zasadę działania i najprostszą możliwą implementację, dlatego nie wspominałem o tym. Do pierwszych projektów można przecież granice całkowania zastąpić zerowaniem zapisanych wartości po każdym/wielu cyklach. Wiadomo, nie jest to najlepsze rozwiązanie, ale na początek wystarczy :)
Fajny tekst, czekamy na kolejne części.
Gdyby ktoś potrzebował gotowej biblioteki regulatora PID: http://playground.arduino.cc/Code/PIDLibrary
Mała uwaga co do wyjścia , nie powinło być tak
U = Kp*(en + (1/Ti)*C*dt/1000 + Td*(en – ep)*dt/1000) ???
tzn. tak
U = Kp*(en + (1/Ti)*C*(dt/1000) + Td*(en – ep)/(dt/1000)) ???
Zwróć uwagę, że już przy liczeniu „C” jest wykonywane mnożenie przez „dt”.
C += ((ep + en)/2)*dt;
W zasadzie można wciągnąć dzielenie przez 1000 do wyliczania C. Taki zapis będzie znacznie bardziej elegancki, dzięki, że zwróciłeś na to uwagę :)
C += ((ep + en)/2)*(dt/1000);
Co do części różniczkującej – dzielenie to inaczej mnożenie przez odwrotność, te dwa zapisy są równoważne: (en-ep)/dt/1000 to (en-ep)*1000/dt
No w sumie masz racje , nie zauważyłem tego :D , myślałem że coś jest źle , uważam że bardziej czytelnie jest taki zapis :
U = Kp*(en + (1/Ti)*C*(dt/1000) + Td*(en – ep)/(dt/1000)) widać ,że tu (dt/1000) jest zamieniane jednostki na [s]
, ale jak kto woli :D
Hmm…. Muszę popracować nad czytelnością kodu :P Dzięki za uwagę, mam nadzieję, że kolejne posty będą lepsze pod tym względem.
Mi najbardziej się podobają te akademickie nazwy zmiennych ;-)
Witam,
mógł by ktoś wrzucić krótki poradnik jak odczytać wagę na arduino przy użyciu SEN-10245 Load Sensor – 50kg. Bardzo proszę o pomoc. Pozdrawiam.
Dzięki za świetny artykuł! Kiedy można spodziewać się kontynuacji tematu?
Hej, dzięki za feedback ;) Szczerze mówiąc to nie wiem, ostatnio mam dosyć pracowity czas na uczelni. Mam nadzieję, że niebawem znajdę trochę więcej czasu na projekty :)
szukałem PID do nagrzewnicy elektrycznej.
W przeciągu tygodnia sprawdzę jak ze strojeniem.
jestem ciekaw jak zadziała.
widzę, że brak mi czasem odwagi samemu przenieść wzór na program
Czesc !
będzie jakiś kolejny artykuł poruszający regulatory PID ?
W tej chwili nie planujemy.