Akcelerometry, żyroskopy i kompasy czyli badanie położenia z Arduino cz. 1
Ostatnio bardzo popularne stały się różnego rodzaju czujniki położenia. Jest to spowodowane głównie za sprawą smartfonów w nie wyposażonych, kontrolerów gier (np Wiimote) lub quadkopterów, którym potrzebne są do stabilizacji lotu. W tym wpisie dowiesz się jak można je wykorzystać do własnych celów.
Akcelerometr
Akcelerometr to czujnik badający przyspieszenie. Przyspieszenie występuje wtedy, kiedy jakaś rzecz zmienia prędkość. Opisuje to druga zasada dynamiki Newtona.
Jeśli jadąc samochodem naciśniesz na “gaz”, to samochód zacznie przyśpieszać, bo silnik zadziałał na niego większą siła przezwyciężając inną siłę – siłę tarcia, która stara się samochód zatrzymać.
Jeśli puścisz pedał “gazu”, to znowu siła tarcia będzie większa i będzie dążyła do zatrzymania samochodu. Czyli przyspieszenie będzie ujemne.
Jest jeszcze jedna siła. Siła grawitacji, która nie pozwala by samochód odfrunął, bo dociska go do ziemi. Siła grawitacji powoduje, że wszystko spada na ziemie z takim samym przyspieszeniem 9,81 m/s2. Ta siła oznaczona jest jednostką 1 g (nie mylić z gramem).
Ta jednostka symbolizuje, że coś działa na jakąś rzecz z siłą grawitacji. W samolotach przy wykonywaniu manewrów siły działające na pilota dochodzą do 9 g. Popularnie się wtedy mówi, że jego ciało waży wtedy 9 razy więcej niż na ziemi. Za to na orbicie Ziemi panuje siła 0 g. Dlatego przedmioty mogą tam swobodnie latać.
Akcelerometr mierzy te siły w jednostkach g. Najpopularniejsze dziś akcelerometry 3-osiowe to tak naprawdę 3 akcelerometry w jednym układzie ułożone tak, by mierzyć przyspieszenie w 3 różnych kierunkach. W dół, w bok i do przodu. Kierunki te nazywane są osiami X, Y i Z i tak określają je twórcy urządzeń.
Jeśli zadziałasz na czujnik przyspieszeniem o przeciwnym kierunku niż został skierowany czujnik, to on zwróci nam wartość przyspieszenia jako ujemną.
Czujnik przyspieszenia i matematyka
Jeśli czujnik leży nieruchomo na ziemi, to wskazuje tylko siłę grawitacji skierowaną w dół do środka Ziemi.
W czujnikach 3-osiowych ta właściwość pozwala na określenie kąta pod jakim jest urządzenie względem ziemi. Wystarczy sprawdzić z jaką siłą grawitacja działa na poszczególne czujniki.
Zakładając, że czujnik skierowany w lewo to X, w przód to Y, a w dół to Z, to akcelerometr leżąc płasko na ziemi, powinien zwrócić wartości:
X = 0g
Y = 0g
Z = 1g
Oznacza to, że dół urządzenia skierowany jest do ziemi.
Natomiast jeśli przechylisz urządzenie na lewy bok, to czujniki pokażą:
X = 1g
Y = 0g
Z = 0g
Jak widzisz siła grawitacji przestała działać na czujnik Z i zaczęła działać z pełną siłą na czujnik X.
A co będzie, jeśli przechylisz urządzenie między ziemią i lewym bokiem (o kąt 45°)?
X = 0.7g
Y = 0g
Z = 0.7g
Okazało się, że grawitacja podzieliła po równo siły na czujnik X i na czujnik Z. Im urządzenie jest skierowane bardziej dołem do ziemi, tym większa jest wartość Z, a mniejsza wartość X. Im urządzenie jest skierowane bardziej lewym bokiem tym większa wartość X, a mniejsza Z.
Jeśli zaczniesz przechylać urządzenie na prawy bok, to czujnik X zacznie zwracać wartości ujemne, bo siła grawitacji będzie działać w jego drugim kierunku. Jeśli położysz urządzenie górą do ziemi to czujnik Z zwróci wartość -1.
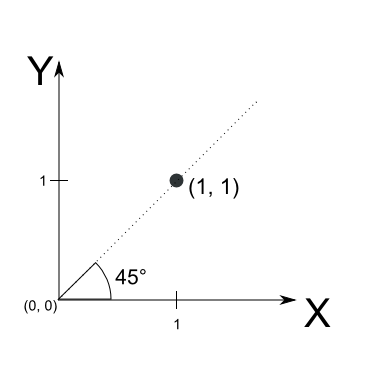
Specjalną funkcją trygonometryczną występującą w wielu językach programowania jest “atan2(y, x)”, przetwarzająca te wartości na dokładny kąt przechylenia urządzenia.
Funkcja ta bierze współrzędne punktu x, y i podaje pod jakim kątem jest ten punkt względem środka układu współrzędnych czyli punktu o współrzędnych 0, 0.
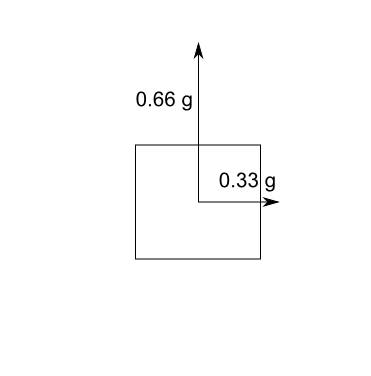
Jak zapewne wiesz w fizyce wartość siły określa się długością strzałki zwanej “wektorem”. Jej kierunek czyli “zwrot” to kierunek w jakim działa siła.
Jeśli na coś działa kilka sił w różnych kierunkach, to od tego odchodzi kilka wektorów w różnych kierunkach o określonej długości.
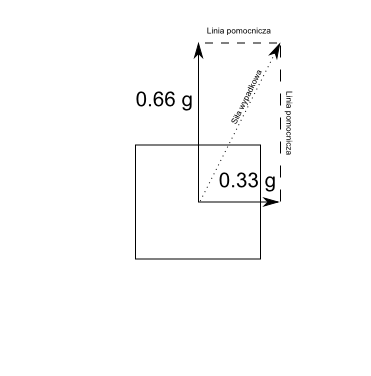
Jednak wynikiem działania tych sił jest wypadkowa siła działająca w jednym kierunku. Siłę tą można wyznaczyć poprzez “złożenie” innych sił, za pomocą linii pomocniczych. Ich przecięcie wyznaczy wypadkową siłę działającą na coś.
Możesz to sobie wyobrazić tak, że kwadrat jest samolotem, który leci w kierunku dłuższego wektora i wieje na niego boczny wiatr z kierunku krótszego wektora i go spycha. Czyli tak na serio samolot będzie leciał zgodnie z kierunkiem wektora siły wypadkowej.
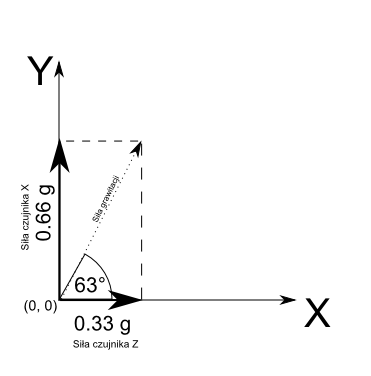
Tak samo jest i w akcelerometrze. Jego czujniki zwracają wartości, które można przedstawić jako długości wektorów. Te wektory mają kierunek zgodny z kierunkiem czujników. Siłę wypadkową w przypadku akcelerometru wyznaczać będzie kierunek działania siły grawitacji, czyli kąt urządzenia względem ziemi.
To pozwala na proste użycie funkcji “atan2” do ustalenia kierunku siły wypadkowej złożonej z wartości sił poszczególnych czujników.
Wykorzystanie funkcji atan2
W jezyku programowania Python funkcja “atan2” znajduje się w module funkcji matematycznych “math”. Można ją testować podstawiając pod jej argumenty różne wartości z powyższych przykładów (argument “x” to wartość czujnika “Z”, a argument “y” to wartość czujnika “X”).
import math
print "Dol urzadzenia jest skierowany do ziemi"
print math.atan2(0, 1)
print "Lewy bok urzadzenia jest skierowany do ziemi"
print math.atan2(1, 0)
print "Urzadzenie skierowane w polowie miedzy ziemia i lewym bokiem"
print math.atan2(0.5, 0.5)
print "Urzadzenie skierowane jak w ostatnim przykladzie dzialania sil"
print math.atan2(0.66, 0.33)
Wynik działania programu może niektórym wydawać się dziwny:
Dol urzadzenia jest skierowany do ziemi
0.0
Lewy bok urzadzenia jest skierowany do ziemi
1.57079632679
Urzadzenie skierowane w polowie miedzy ziemia i lewym bokiem
0.785398163397
Urzadzenie skierowane jak w ostatnim przykladzie dzialania sil
1.10714871779Nie są to wartości przedstawione w stopniach. Są przedstawione w radianach.
Radian to jednostka kąta (używana w nauce i programowaniu), w której kąt zamiast w stopniach przedstawiany jest w wielokrotności liczby PI. Liczba PI czyli około 3,1415 odpowiada kątowi 180°. Połowa liczby PI czyli 1.57 to połowa kąta 180° czyli 90°. Tak samo jak 2*PI to kąt 2*180° czyli 360°.
Radiany przelicza się bardzo łatwo na stopnie. Służy do tego wzór:
stopnie = radiany * 180 / PIMożna też użyć specjalnej funkcji języka Python, która przerabia radiany na stopnie. Nosi ona nazwę “degrees” i jest z modułu “math”.
import math
print "Dol urzadzenia jest skierowany do ziemi"
print math.degrees(math.atan2(0, 1))
print "Lewy bok urzadzenia jest skierowany do ziemi"
print math.degrees(math.atan2(1, 0))
print "Urzadzenie skierowane w polowie miedzy ziemia i lewym bokiem"
print math.degrees(math.atan2(0.5, 0.5))
print "Urzadzenie skierowane jak w ostatnim przykladzie dzialania sil"
print math.degrees(math.atan2(0.66, 0.33))Teraz wynik działania programu jest już bardziej zrozumiały i zgadza się z wcześniejszym teoretyzowaniem.
Dol urzadzenia jest skierowany do ziemi
0.0
Lewy bok urzadzenia jest skierowany do ziemi
90.0
Urzadzenie skierowane w polowie miedzy ziemia i lewym bokiem
45.0
Urzadzenie skierowane jak w ostatnim przykladzie dzialania sil
63.4349488229Wspomne jeszcze o dwóch rodzajach kątów. Na co dzień przyzwyczajeni jesteśmy przez szkołę, że istnieją kąty od 0 do 360°. Jenak nie jest tak zawsze. Często też liczy się tak, że kąty na prawo od 0° to 1°, 2°, 3° … 180°, a na lewo to -1°, -2°, -3° … -179°. Zatem zamiast 181° jest -179°, a zamiast 359° jest -1°.
W Arduino używanie funkcji “atan2” jest podobne, z tą różnicą, że nie ma funkcji konwertującej na stopnie, dlatego zastosowałem wzór.
void setup() { Serial.begin(9600); Serial.println(F("Dol urzadzenia jest skierowany do ziemi")); Serial.println(atan2(0, 1) * 180 / PI); Serial.println(F("Lewy bok urzadzenia jest skierowany do ziemi")); Serial.println(atan2(1, 0) * 180 / PI); Serial.println(F("Lewy bok urzadzenia jest skierowany do ziemi")); Serial.println(atan2(0.5, 0.5) * 180 / PI); Serial.println(F("Urzadzenie skierowane jak w ostatnim przykladzie dzialania sil")); Serial.println(atan2(0.66, 0.33) * 180 / PI); } void loop() { }
Czujnik przyspieszenia ADXL345
Wiele płytek z czujnikami w ofercie Nettigo ma w sobie czujnik przyspieszenia ADXL345. Jest to cyfrowy czujnik przyspieszenia. Pracuje on w standardzie 3,3V. Komunikuje się za pomocą interfejsów TWI (i2c) lub SPI. Czujnik może mierzyć przyspieszenia do +/- 16 g. Przy pełnym zakresie pomiarów rozdzielczość wynosi 13 bitów, a dokładność 0,004 g. Jednak można też zawęzić zakres pomiarowy do +/- 2/4/8/16 g i rozdzielczość do 10 bitów w ten sposób zmniejszając dokładność. Czujnik może mierzyć przyspieszenie z częstotliwością od 6,25 do 3200 razy na sekundę. Urządzenie ma bufor FIFO. Pozwala on na to, żeby procesor nie musiał odczytywać wyników w określonym czasie wyznaczonym przez częstotliwość, tylko odczytał je potem w większej ilości na raz.
Podłączenie czujnika ADXL345
Czujnik występujący na płytkach ma zazwyczaj wyprowadzone piny magistrali i2c i zasilania. Zasilanie wynosi 3,3V i w takim też standardzie działa płytka. Jeśli chcesz podłączyć ja do Arduino musisz zastosować dwukierunkowy konwerter poziomów logicznych opisany w poprzednim wpisie.
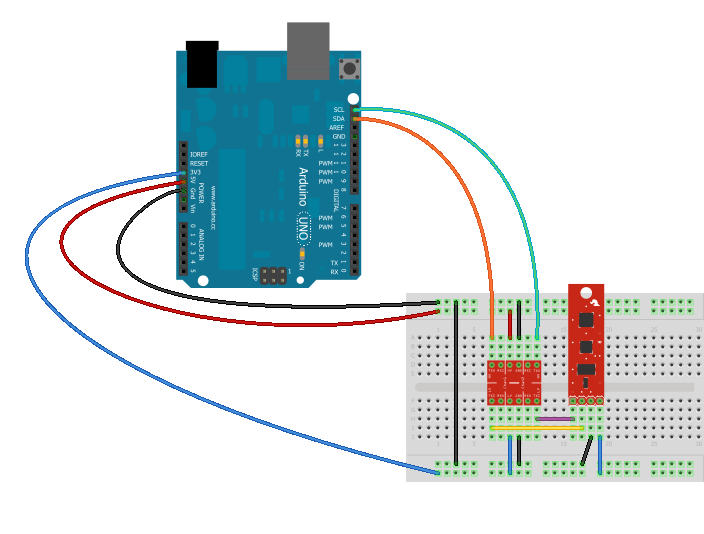
Wyjście magistrali TWI w nowym Arduino UNO R3 znajduje się tak jak na rysunku nad pinem AREF.
W starszych płytkach magistrala miała wyprowadzenia w grupie pinów ANALOG IN. Sygnał SDA jest w pinie Analog In 4, a sygnał SCL jest w Analog In 5.
W Arduino MEGA sygnały TWI są w grupie pinów COMMUNICATION. Sygnał SDA to pin 20, a SCL to pin 21.
Wyjście magistrali TWI (i2c) w standardzie 5V podłączone są do dwukierunkowych wejść konwertera poziomów logicznych za pomocą przewodów pomarańczowego (SDA) i zielonego (SCL).
Do konwertera podłączone jest też zasilanie 5V (czerwony przewód) i 3,3V (niebieski przewód). Masa czyli GND podłączona jest czarnym przewodem.
Dwukierunkowe wyjście magistrali TWI z konwertera w standardzie 3,3V oznaczone jest przewodem fioletowym (SCL) i żółtym (SDA), które wraz z zasilaniem 3,3V (niebieski przewód) i GND (czarny przewód) trafia do czujnika.
Ponieważ jest wiele wersji płytek czujników, musisz sam sprawdzić w jego dokumentacji do jakich pinów trafiają jakie sygnały. W przykładzie wybrałem płytkę najbardziej rozbudowanego czujnika 9dof.
Programowanie czujnika ADXL345
Do sterowania czujnikiem najlepiej użyć wbudowanej w Arduino IDE biblioteki “Wire.h”. Zapewnia ona komunikację z urządzeniami magistrali i2c (TWI).
Biblioteka udostępnia obiekt o nazwie “Wire” przez który wywołujemy różne metody obsługujące magistralę. W funkcji “setup” należy najpierw wywołać metodę “Wire.begin()” przygotowującą bibliotekę do działania.
#include <Wire.h> void setup() { Wire.begin(); }
Aby wysłać coś do urządzenia potrzebne są kolejne 3 metody.
-
“Wire.beginTransmission(adres)”, która przygotowuje przesyłanie danych do urządzenia, którego adres (numer identyfikacyjny określający do którego urządzenia wysyła się dane) jest argumentem metody.
-
“Wire.write(dane)”, która wysyła dane do urządzenia.
-
“Wire.endTransmission()”, która kończy wysyłanie danych do wybranego urządzenia.
Czujnik ADXL348 ma adres w magistrali TWI o numerze szesnastkowym 0x53. Czujnik ten ma kilkanaście rejestrów. Rejestry to takie sprzętowe zmienne wewnątrz urządzenia, które ustawiają parametry działania urządzenia i przechowują wyniki jego pracy. Aby zapisać coś do rejestru, trzeba wysłać do urządzenia 2 bajty. Pierwszym jest numer rejestru, a kolejnym wartość jaką trzeba zapisać do rejestru.
Ponieważ czujnik wymaga ustawienia kilku rejestrów napisałem specjalną funkcję ustawiającą rejestr.
void twiSetRegister(int address, byte reg, byte data) { // przygotowanie transmisji Wire.beginTransmission(address); // wysylanie numeru rejestru Wire.write(reg); // wysylanie wartosci do zapisania w rejestrze Wire.write(data); // koniec transmisji Wire.endTransmission(); delay(5); }
Argumenty tej funkcji to adres urządzenia, numer rejestru i wartość do zapisania w tym rejestrze.
Aby uruchomić czujnik trzeba ustawić 3 rejestry.
Rejestr o numerze 0x2d to jakby włącznik czujnika. Ustala on czy urządzenie ma działać czy być w trybie uśpienia regulując tym samym jego pobór prądu. Bity tego rejestru oznaczają:
|
D7 |
D6 |
D5 |
D4 |
D3 |
D2 |
D1 |
D0 |
|
0 |
0 |
Link |
AUTO_SLEEP |
Measure |
Sleep |
Wakeup1 |
Wakeup0 |
Bit Link ustawia urządzenie w tryb nieaktywności, i pomiary są robione dopiero kiedy procesor potwierdzi, że chce je otrzymać.
Bit AUTO_SLEEP ustawia czujnik w tryb oszczędzania energii, z którego wychodzi po wykryciu przyspieszenia o jakiejś minimalnej wartości.
Bit Measure włącza tryb normalnej pracy czujnika. Czujnik robi ciągle pomiary i zapisuje ich wyniki w odpowiednich rejestrach.
Bit Sleep przełącza urządzenie w tryb oszczędzania energii
Bity Wakeup regulują czas, co jaki urządzenie w trybie oszczędzania energii ma się budzić i sprawdzać przeciążenie. Od 1 do 8 razy na sekundę.
W programie ustawiam ten rejestr na wartość 0x08 czyli binarnie 00001000. Oznacza to, że włączę tylko bit Measure rejestru. Przestawi to czujnik w tryb ciągłego pomiaru bez żadnego oszczędzania energii.
Rejestr o numerze 0x31 ustala w jakim formacie mają być wyniki pomiarów czujnika.
|
D7 |
D6 |
D5 |
D4 |
D3 |
D2 |
D1 |
D0 |
|
SELF_TEST |
SPI |
INT_INVERT |
0 |
FULL_RES |
Justify |
Range1 |
Range0 |
Bit SELF_TEST służy do testowania czujnika. Po jego włączeniu zamiast normalnych wartości pomiarów zwraca specjalne liczby, których zakres jeśli się zgadza z dokumentacją, to czujnik jest dobry.
Bit SPI służy do ustawiania trybu pracy magistrali SPI. Jeśli jest włączony to magistrala jest 3 przewodowa (sygnał danych jest 2 kierunkowy), jeśli wyłączony to magistrala jest standardowa 4 przewodowa z 2 przewodami przesyłania danych.
Bit INT_INVERT określa czy wyjście przerwania jest aktywne w stanie wysokim (bit włączony) lub aktywne w stanie niskim (bit wyłączony).
Bit FULL_RES włącza tryb pełnej rozdzielczości czujnika (13 bitów), gdzie wynik ma dokładnośc 0,004 g na jednostkę. Wyłączenie bitu skaluje wynik na wartość 10 bitową, której zakres ustala się kolejnymi bitami.
Bit Justify. Wynik pomiaru w zależności bitu FULL_RES jest 10 albo 13 bitowy. Rejestry z wynikiem są 2*8 bitów czyli 16 bitowe. Włączenie tego bitu powoduje, że wynik będzie zapisany od ostatniego bitu rejestru wyniku (binarnie nnnnnnnnnn000000 n-to bity wyniku), a wyłączenie, że od pierwszego (binarnie 000000nnnnnnnnnn).
Bity Range0 i Range1 ustalają zakres pomiarów czujnika od +/-2 do +/-16 g. Zakres ten pozwala określić dokładność w jakiej pracuje czujnik w trybie 10 bitowym. Np. dla zakresu +/-2g dokładność wyjścia 10 bitów (1024 poziomy) będzie wynosiła(od -2 do 2 są 4 jednostki) 4 / 1024 = 0,004 g czyli taka sama jak w trybie “FULL_RES”. Dla kolejnych zakresów dokładność będzie spadała z każdym krokiem o połowę.
W programie ustawiłem ten rejestr na wartość szesnastkową 0x08 czyli binarnie 00001000. Oznacza to włączony tylko bit FULL_RES ustawiający wyjścia na dokładność 0.004g na jednostkę.
Rejestr o numerze 0x2c ustawia częstotliwość z jaką czujnik ma mierzyć przyspieszenie.
|
D7 |
D6 |
D5 |
D4 |
D3 |
D2 |
D1 |
D0 |
|
0 |
0 |
0 |
LOW_POWER |
Rate3 |
Rate2 |
Rate1 |
Rate0 |
Bit LOW_POWER włącza tryb oszczędzania energii (o 30%). W tym trybie pomiar może być wykonywany normalnie, lecz jest bardziej zaszumiony.
Bity Rate3..Rate0 określają cześtotliwość pomiarów (w Hz) z jaką wyniki będą zapisywane do rejestrów.
|
Częstotliwość |
Rate3 |
Rate2 |
Rate1 |
Rate0 |
|
3200 |
1 |
1 |
1 |
1 |
|
1600 |
1 |
1 |
1 |
0 |
|
800 |
1 |
1 |
0 |
1 |
|
400 |
1 |
1 |
0 |
9 |
|
200 |
1 |
0 |
1 |
1 |
|
100 |
1 |
0 |
1 |
0 |
|
50 |
1 |
0 |
0 |
1 |
|
25 |
1 |
0 |
0 |
0 |
|
12,5 |
0 |
1 |
1 |
1 |
|
6,25 |
0 |
1 |
1 |
0 |
Rejestr ten ustawiłem na wartość 0x09 czyli binarnie 00001001, co daje częstotliwość pomiarów 50 razy na sekundę.
Rozwinięty program z ustawianiem rejestrów wygląda tak:
#include <Wire.h> // Adres czujnika #define ADXL_ADDR 0x53 // Funkcja ustawiania rejestru void twiSetRegister(int address, byte reg, byte data) { Wire.beginTransmission(address); Wire.write(reg); Wire.write(data); Wire.endTransmission(); delay(5); } void setup() { Wire.begin(); // Ustawianie rejestrow twiSetRegister(ADXL_ADDR, 0x2d, 0x08); twiSetRegister(ADXL_ADDR, 0x31, 0x08); twiSetRegister(ADXL_ADDR, 0x2c, 0x09); } void loop() { }
Po uruchomieniu programu czujnik powinien działać już prawidłowo jednak do pełni szczęścia zostało…
Odczytywanie danych z czujnika ADXL345
Wyniki pomiarów czujnika to liczby typu “int” (16 bitowa wartość ze znakiem [+/-]). Ponieważ rejestry czujnika są 8 bitowe, to wynik przechowywany jest w 2 rejestrach dla każdego kierunku. W pierwszym są bity od 0 do 7 (zwane też LSB), a w drugim od 8 do 15 (zwane też MSB).
Za zamianę 2 zmiennych 8 bitowych na jedną 16 bitową odpowiada funkcja “word(h, l)”. Jej pierwszym argumentem jest zmienna 8 bitowa przechowująca bity od 8 do 15, a drugim zmienna trzymająca bity od 0 do 7. Można ją wykorzystać tak:
int wynik = word(rejestr1, rejestr0);
Jeśli jest ustawiony bit FULL_RES rejestru 0x31 to jednostka wyniku daje dokładność 0,004 g. Co można łatwo przeliczyć na siłę w jednostkach g.
float sila_g = wynik * 0.004;
Do odebrania danych z rejestrów musisz poznać kolejne 3 metody obiektu “Wire”.
-
“Wire.requestFrom(adres, ilosc)” – przygotowuje magistrale TWI do odbioru danych z urządzenia o adresie podanym w pierwszym argumencie, a ilość danych do odbioru określa się w drugim argumencie.
-
“Wire.available()” – zwraca ilość bajtów oczekujących na odebranie.
-
“Wire.read()” – zwraca jeden bajt danych odebranych z magistrali TWI.
Przygotowałem funkcję ułatwiającą odczyt kilku rejestrów napisaną na podstawie tych metod.
byte twiGetRegisters(int address, byte reg, byte *buffer, byte length) { // liczinik odebranych danych byte count = 0; // wyslanie numeru pierwszego rejestru Wire.beginTransmission(address); Wire.write(reg); Wire.endTransmission(); // odbieranie wartosci z rejestrow Wire.beginTransmission(address); Wire.requestFrom(address, (int) length); while (Wire.available()) { buffer[count] = Wire.read(); count++; } Wire.endTransmission(); // zwracanie ilosci odebranych danych return count; }
Argumenty tej funkcji to adres urządzenia z którego chcesz pobrać dane, numer rejestru od którego chcesz zacząć pobieranie, nazwa tablicy do której mają być zapisane dane i ilość danych do odczytania.
Funkcja zwraca liczbę odczytanych rejestrów.
Rejestry z wynikami zaczynają się od numeru 0x32. Ułożone są parami x0, x1, y0, y1, z0, z1.
#include <Wire.h> // Adres czujnika #define ADXL_ADDR 0x53 // Funkcja ustawiania rejestru void twiSetRegister(int address, byte reg, byte data) { Wire.beginTransmission(address); Wire.write(reg); Wire.write(data); Wire.endTransmission(); delay(5); } // Funkcja odczytywania rejestrow byte twiGetRegisters(int address, byte reg, byte *buffer, byte length) { byte count = 0; Wire.beginTransmission(address); Wire.write(reg); Wire.endTransmission(); Wire.beginTransmission(address); Wire.requestFrom(address, (int) length); while (Wire.available()) { buffer[count] = Wire.read(); count++; } Wire.endTransmission(); return count; } void setup() { Wire.begin(); // Ustawianie rejestrow twiSetRegister(ADXL_ADDR, 0x2d, 0x08); twiSetRegister(ADXL_ADDR, 0x31, 0x08); twiSetRegister(ADXL_ADDR, 0x2c, 0x09); // Ustawienie komunikacji z komputerem Serial.begin(57600); } void loop() { // tablica do zapisywania danych z rejestrow byte buffer[6]; // odczytywanie 6 rejestrow do tablicy buffer byte readed = twiGetRegisters(ADXL_ADDR, 0x32, buffer, 6); // sprawdzenie czy odebrano 6 rejestrow if (readed != 6) { // jesli nie to wyswietl error Serial.println(F("ERROR")); } else { // jesli tak to wyswietl wartosc pomiaru akcelerometru Z //odczytywanie wartosci cyfrowej z akcelerometru int result = word(buffer[5], buffer[4]); // zamiana cyfrwej wartosci na jednostke g float g_force = result * 0.004; Serial.println(g_force); } // oczekiwianie na kolejny wynik 20 ms czyli 1/50 s // dla czujnika ustawionego na 50 pomiarow/s delay(20); }
Program odczytuje wartość pomiaru z czujnika przyśpieszenia “Z” i wyświetla w jednostkach g. Jeśli czujnik leżał płasko na ziemi to powinien zwracać wartość około 1.00 g. Wraz z przechylaniem czujnika wartość ta powinna maleć.
Odczytywanie przechylenia i pochylenia czujnika
Na początku wpisu opisałem funkcję “atan2(y, x)”. Teraz przyszedł czas na jej wykorzystanie.
Kąt przechylenia (na boki) obliczasz składając wektory czujników “X” i “Z”.
float roll = atan2(gX, gZ) * 180 / PI;
Kąt pochylenia (do przodu i do tyłu) obliczasz składając wektory czujników “Y” i “Z”.
float pitch = atan2(gY, gZ) * 180 / PI;
W ten sposób możesz przerobić funkcję “loop” programu do odczytywania kąta położenia urządzenia względem Ziemi.
void loop() { byte buffer[6]; byte readed = twiGetRegisters(ADXL_ADDR, 0x32, buffer, 6); if (readed != 6) { Serial.println(F("ERROR")); } else { // odczytanie wartości pomiarów int resultX = word(buffer[1], buffer[0]); int resultY = word(buffer[3], buffer[2]); int resultZ = word(buffer[5], buffer[4]); // zamiana na jednostki g float gX = resultX * 0.004; float gY = resultY * 0.004; float gZ = resultZ * 0.004; // obliczenie przechylenia float roll = atan2(gX, gZ) * 180 / PI; // obliczenie pochylenia float pitch = atan2(gY, gZ) * 180 / PI; // wyslanie danych do komputera Serial.print(roll); // przechylenie Serial.print(","); Serial.println(pitch); // pochylenie } delay(20); }
Program powinien zwracać w “Serial Monitor” (pamiętaj o ustawieniu 57600 bodów) 2 liczby rozdzielone przecinkiem. Pierwsza to kąt przechylenia, a druga to kąt pochylenia.
Praktyczne wykorzystanie
Byś mógł lepiej prześledzić działanie czujnika, napisałem za pomocą języka Python i modułów “pyserial” i “PyGtk2” program wizualizujący jego działanie. Program składa się z 3 widgetów. Pierwszym jest wyświetlanie przyspieszeń w 3 osiach. Widget jest podobny do tego wykorzystywanego kiedyś w transmisjach F1 pokazujący przeciążenia działające na kierowce.
Drugim widgetem jest znany z samolotów sztuczny horyzont pokazujący przechylenie i pochylenie samolotu względem ziemi.
Trzecim widgetem jest symulacja znanej u majsterkowiczów poziomnicy, którą się przykłada do różnych konstrukcji, by sprawdzić czy trzymają poziom.
Żółty wskaźnik to wektor siły z akcelerometru “X”, czerwony/zielony akcelerometru “Y”, a niebieski “Z”.
Program wymaga, aby Arduino dostarczyło do komputera odpowiednie dane o siłach przyspieszenia, pochyleniu i przechyleniu w formacie:
#ACC=fx,fy,fz,roll,pitch\r\nDlatego przerobiłem funkcję “loop” z ostatniego przykładu na taką:
void loop() { byte buffer[6]; byte readed = twiGetRegisters(ADXL_ADDR, 0x32, buffer, 6); if (readed != 6) { Serial.println(F("ERROR")); } else { int resultX = word(buffer[1], buffer[0]); int resultY = word(buffer[3], buffer[2]); int resultZ = word(buffer[5], buffer[4]); float gX = resultX * 0.004; float gY = resultY * 0.004; float gZ = resultZ * 0.004; float roll = atan2(gX, gZ) * 180 / PI; float pitch = atan2(gY, gZ) * 180 / PI; Serial.print(F("#ACC=")); Serial.print(gX); Serial.print(","); Serial.print(gY); Serial.print(","); Serial.print(gZ); Serial.print(","); Serial.print(roll); Serial.print(","); Serial.println(pitch); } delay(20); }
Program w Pythonie do uruchomienia wymaga tylko jednej drobnej zmiany. Ustalenia w zmiennej “ACC_PORT” na początku pliku, nazwy portu szeregowego do którego podłączyłeś Arduino.
ACC_PORT = 'com4:'Kalibracja akcelerometru
Świat nie jest idealny. Montując czujnik w urządzeniu nie masz gwarancji, że umieścisz go tam idealnie prosto, lub wymaga to zbyt wiele wysiłku. Kładąc potem urządzenie na wypoziomowanym podłożu może się okazać, że czujnik wskazuje jakiś kąt przechylenia/pochylenia. Taka sytuacja wymaga kalibracji czujnika.
Korekcja polega na dodaniu lub odjęciu jakiejś wartości od wyników czujnika tak, żeby podawał wartości jakich oczekujesz.
Do korekcji osi czujników służą specjalne rejestry o numerach 0x1e, 0x1f, 0x20 odpowiadające osiom “X”, “Y”, “Z”. Pozwalają one dodać lub odjąć jakąś wartość do rejestrów wynikowych czujnika. Maksymalną korekcję jaką można dokonać to +/- 2g. Rejestry przyjmują wartości 8 bitowe ze znakiem, czyli typ “char” (przechowujący liczby od -128 do 127). Minimalna jednostka z jaką można przesunąć wartość wyniku to:
2.0 / 128 = 0.015625 gJeśli moje urządzenie leżąc płasko na ziemi ma wyniki X:0,05g, Y:-0,11g, Z:1,0g, to oprócz “Z”, które jest prawidłowo, trzeba przesunąć inne o odwrotną wartość, czyli:
X: -0,05 / 0,015625 = -3 Y: 0,11 / 0,015625 = 7 Zatem do rejestru 0x1e trzeba wpisać liczbę -3, do 0x1f trzeba wpisać 7, a do 0x20 trzeba wpisać 0.
void setup() { Serial.begin(57600); Wire.begin(); twiSetRegister(ADXL_ADDR, 0x2d, 0x08); twiSetRegister(ADXL_ADDR, 0x31, 0x08); twiSetRegister(ADXL_ADDR, 0x2c, 0x09); // kalibracja twiSetRegister(ADXL_ADDR, 0x1e, (char) -3); twiSetRegister(ADXL_ADDR, 0x1f, (char) 7); twiSetRegister(ADXL_ADDR, 0x20, (char) 0); }
Typ “(char)” w nawiasie określa jakiego typu mają być liczby przekazywane w argumencie.
Innym rodzajem kalibracji jest określenie, czy każdy czujnik po skierowaniu w kierunki grawitacji i w przeciwnym ma takie same wielkości wartości (czyli 1.0g i -1.0g). Jeśli się różnią to trzeba je odpowiednio przeskalować.
Zakładając, że przy dokładności 0.004 g, wartość cyfrowa czujnika czyli zmiennej “resultX” dla 1g wynosi 1 / 0.004 = 250
Jeśli czujnik “X” skierowany w kierunku grawitacji zwracałby wartość cyfrową 256, a w przeciwnym -270, to należałoby go skalibrować za pomocą takiego algorytmu:
if (resultX >= 0) { resultX = map(resultX, 0, 256, 0, 250); } else { resultX = map(resultX, -270, 0, -250, 0); }
Wykorzystałem tu funkcje skalującą “map” z biblioteki Arduino. Funkcja ta przetwarza zakres wartości jakimi dysponujesz (argumenty 0, 256), na wartości jakich oczekujesz (argumenty 0, 250). Dzięki temu jeśli czujnik skierowany w kierunku grawitacji zwróci 256, to funkcja “map” przerobi tą wartość na 250 czyli 1g.
Niedoskonałości czujnika przyspieszenia
Czujnik przyspieszenia nie jest idealnym rozwiązaniem do badania położenia. O tym samym przekonani się producenci telefonów i konsol. Wystarczy, że nim potrząśniesz (czyli dodasz kilka wektorów przyspieszenia), a już gubi kierunek grawitacji. Można próbować to eliminować różnymi filtrami i algorytmami, ale one tylko spowalniają pomiar, a tym samym szybkość reakcji urządzenia na zmianę położenia.
Inną niedogodnością jest to, że sam czujnik przyspieszenia wykrywa tylko przechylenie i pochylenie (pitch i roll), ale nie wykrywa odchylenia (yaw) czyli kierunku wg stron świata.
Te niedogodności rozwiązują inne czujniki (znajdujące się zwykle na płytkach z akcelerometrem), które opiszę w kolejnych odcinkach.



kolejny genialny wpis, mam jednak problem z zasubskrybowaniem RSS z nagłówkami, ten z komentarzami działa bezbłędnie. Mam Operę w najnowszej stabilnej wersji.
Witam
Pisze tu bo nie wiem kto by był w stanie mi pomóc. Na mojej uczelni nikt nie ogarnia tematu;p Piszę program do stabilizacji lotu i mam problem z odczytywaniem sygnału z kontrolera. Program działa ale strasznie wolno. Sygnał z nadajnika(kontrolera) zczytuje w ten sposób:
float read_RX(int N)
{
int val2 = pulseIn(N, HIGH);
if (val2 == 0 || val2 2000)
{
return val2;
}
float deg = map(val2, 1000, 2000, 0, 180);
deg = constrain (deg, 0, 180);
Serial.println(deg);
return deg;
}
gdzie N jest sygnałem z nadajnika.
read_RX(int N) podstawiam jako wartośc do której donzy układ stabilizacji. Jeżeli ktoś jest w stanie pomoc prosze o kontakt. Mam termin z tym a juz kur….wica strzela;(
Michał: Bardzo dziękuję za słowa uznania! Pomogą mi one w opracowywaniu dalszych artykułów :-)
Karol: Chętnie ci pomogę. Dokończę komentarz za chwilę, bo mam kilka obowiązków.
Karol: Zapowiada się ciekawy projekt. Kiedyś robiłem podobny, ale sterowanie było z tabletu i ominęła mnie przyjemność odczytywania PWM.
Z tego co widzę, to wydaje mi się, że funkcja „pulseIn” nie za bardzo nadaje się do czytania wielu kanałów na raz z odbiornika RC. Doświadczeni piszą, że najwyżej 2. Bo funkcja blokuje działanie programu i czeka na kolejny pełny impuls.
Jako tymczasowe rozwiązanie poleca się dodać 3 argument do funkcji „pulseIn” czyli „timeout” w mikrosekundach.
int val2 = pulseIn(N, HIGH, 50000);
Wydaje mi się, że najlepszym rozwiązaniem jest zbudowaie nieblokującej funkcji czytającej wszystkie kanały na raz.
Trzeba to zrobić tak, że w pętli czytasz po kolei wszystkie piny kanałów. Najlepiej za pomocą definicji „PORTx” zamiast „digitalRead”. I zliczasz jak długo na każdym trwał stan wysoki. Nie blokując programu.
Jak chcesz na to jakies pomysły (ja mam przynajmniej 3) to napisz. Jak sam rozwiążesz to powodzenia :)
Dzięki wielkie.
Metoda prób i błędów doszedłem do wniosku, że poptrzebne są przerwania przy odczytywaniu sygnału z kontrolera, bo regulator się gubił i nie wiedział do jakiej wartości ma dążyć. Na szczęście przerwania nie były potrzebne przy zczytywaniu sygnału z czujnika położenia (zastosowałem akcelerometr i żyroskop), bo pierwszy raz to robiłem i wszyscy doradzali ze int’y nie potrzebne i nie robiłem ścieżek na płytce;p
Przerwania nie są takie straszne :). Chyba, że się przesadzi. Ale czujniki mają też podawanie wyniku na żądanie.
Jakbyś chciał ładnie podzielić program na fragmenty wywoływane z określonym interwałem czasu to tu jest rozwiązanie http://sprae.jogger.pl/2011/10/14/wielozadaniowosc-w-arduino/
@OFFTOPIC
Cześć, mam pytanie. Czy diodę led można podłączyć do pinu PWM i używać tego pinu jak tego bez PWM?
Tak, piny PWM można używać dokładanie tak samo jak cyfrowe bez PWM.
Witam,
Czy jest jakiś sposób, aby podłączyć do Arduino ponad 30 fotorezystorów i odczytywać z nich dane? Czy to za dużo? No i jak rozwiązać problem, kiedy mam właśnie kilkadziesiąt fotorezystorów na wejściu i 2 razy więcej diód led do sterowania?
@Kuba
Bardziej potrzebujesz czegoś jak http://nettigo.pl/products/102 – dwie sztuki dadzą ci 32 wejścia kosztem 5 cyfrowych (3 na SPI i po jednym na CS na każdy układ + dwa analogowe na odczyt wyjść z multiplekserów). Dużą ilość diod to możesz załatwić przez TLC5940 http://nettigo.pl/products/50 + opis tutaj na Starter Kicie: https://starter-kit.nettigo.pl/2012/01/tlc5940-czyli-co-najmniej-16-dodatkowych-pinow-pwm-w-arduino/
Oczywiście diodę przez rezystor :)
Dziękuję za odpowiedź.
@sprae to wiem, już sie przyzwyczaiłem do „Pamiętaj o rezystorze 220om”
P.S Zauważyłem, że błędnie tu piszecie. Nie ohm, a om(źródło pl.wikipedia.org)
Dziękuję, ale mnie użyli zawsze Ohm i na sprzęcie też tak widziałem, z resztą na angielskiej wiki jest tak http://en.wikipedia.org/wiki/Ohm :)
Angielska wiki mówi ohm, polska om (na dole tej strony jest: http://pl.wikipedia.org/wiki/Ohm)
Znalazłem stronę opisującą użycie HMC5883L z ARDUINO UNO
http://bildr.org/2012/02/hmc5883l_arduino/
bez użycia konwertera poziomów logicznych. Proszę o opinię na temat przedstawionego sposobu połączenia, czy jest poprawny, bezpieczny?
Oczywiście możesz tak podłączyć, ale na własną odpowiedzialność :-). Ja się starałem to robić zgodnie z zaleceniami w dokumentacji tak, żeby każdy z was był zadowolony i każdemu działało.
Producent w dokumentacji wspominał o maksymalnym napięciu zasilania 3,6 V i za zachowanie w innych nie bierze odpowiedzialności.
Przepraszam, może brzmię jak biurokrata, a nie hacker, ale to dla dobra czytelników. Sami możecie eksperymentować jak chcecie :) Powodzenia.
Bardzo dziękuje za odpowiedź. Jednak prosiłbym o doprecyzowanie :). Zgodnie z ideogramem na stronie http://bildr.org/2012/02/hmc5883l_arduino/
zasilanie HMC5883L to 3,3V a ty sugerujesz, że może być do 3,6V co może być zabójcze dla HMC ? Czy może chodzi o napięcia jakie będą pojawiać się na Analog A4 i A5. Proszę o wyrozumiałość jeśli nie rozumiem być może czegoś oczywistego.
Tak, chodzi o stany logiczne na magistrali I2C. One są większe niż zasilanie, a to jest niezgodne z dokumentacją czujnika.
Być może w większości przypadków natężenie prądu zasilanie jest na tyle niewielkie, że nie jest w stanie zaszkodzić przy takim napięciu. Tak samo jak można zasilać układy 5V bezpośrednio baterią 9V i zazwyczaj działają normalnie. Lecz jak zamiast baterii użyjesz akumulatorka lub silniejszego zasilacza o takim napięciu, to układy się spalają.
Dlatego wolałem zachować ostrożność.
Bardzo dziękuje, teraz rozumiem naturę rzeczy, w wyżej opisanych warunkach może dojść do zniszczenia HMC w tamtym konkretnym może działać. Ta odpowiedź była bardzo pouczająca. Muszę kupić konwerter poziomów logicznych a nawet dwa :)
Jedna poprawka: atan2 nie jest funkcją trygonometryczną tylko cyklometryczną :)
Kamil: Dziękuję :)
Świetna sprawa!!! Mam pytanie, zajmuję się budowaniem rakiet. Są różnej wielkości. Przyspieszenia jakie tam występują to nawet 50g czy czujnik da radę?
No i druga sprawa, ogólnie układ świetny do tego typu zastosowań. Czy może wspólnie nie pobawilibyśmy się w robienie wyposażenia pokładowego modeli rakiet?
To może być fajna współpraca, a i materiały na stronę będą znakomite!
Co do tego czujnika to nie bardzo – maksymalne przyspieszenie odczytywane przez ADXL345 to +-16g. 50g go nie uszkodzi, ale nie da się odczytać. Jeżeli chodzi o przyspieszenie rzędu 50g to np http://www.sparkfun.com/products/9332 to +- 250g Powinno wystarczyć :)
Bardzo dobry tekst, dzięki sprae!
Gdyby ktoś potrzebował aplikacji pythonowej działającej pod Pythonem 3 i Gtk+ 3 to można znaleźć tutaj: https://gist.github.com/michalzielanski/5806325
Dziękuję :)
Również za port
Świetna robota
Super artykuł. Z takimi materiałami to można się uczyć elektroniki ;-)Szkoda, że nie ma dalszych części, bo stoję przed problemem budowy układu do rejestracji trajektorii różnych części ciała. Teraz już wiem, że sam akcelerometr nie wystarczy. Ktoś ma jakies doświadczenia jakie czujniki trzebaby wykorzystać ?
Pełny (jak na dzisiejsze czasy) czujnik położenia składa się z akcelerometru, żyroskopu i kompasu (magnetometru).
Taki zestaw pozwala na badanie kąta pod jakim znajduje się czujnik względem ziemi z ograniczeniem wpływu przeciążeń związanych z ruchem. Coś jak poziomica 3d ;-).
Nie ma możliwości zbadania o ile się czujnik przemieścił. Tym zwykle zajmuje się GPS.
Google w nowych telefonach zastosowało czujnik zmian pola magnetycznego. Wieść gminna niesie, że on pozwala na badanie przesunięcia. Niestety nie wiem jak dokładnie i czy tylko wskazuje przemieszczanie, czy może prędkość i odległość i w jakich osiach.
No właśnie z tego co zdążyłem sie zorientować to do wyznaczenia położenia potrzeba tych 3 czujników które wymieniłeś. Żaden z nich nie daje na wyjściu przemieszczeń. Dane które się otrzymuje to przyspieszenia liniowe – akcelerometr, prędkości kątowe – żyroskop i orientację kątową w przestrzeni – magnetometr. Żeby z tego wyłuskać przemieszczenie trzeba przyspieszenie 2 razy całkować po czasie i prędkości kątowe raz po czasie, żeby otrzymać kąty. W związku z ograniczoną częstotliwością próbkowania pojawiają się błędy przy całkowaniu, które narastają z czasem. Magnetometr pełni z tego co wiem funkcję kompensującą wynik całkowania. Na razie to rozgryzam na sucho, ale jeszcze jasnego obrazu sytuacji nie mam. U mnie GSM odpada, bo płaszczyzna robocza to sześcian 10-20 cm w zależności od przypadku.
Ciekawe wydają się czujniki indukcyjne, ale póki co spotkałem się na razie z takimi które mierzą przemieszczenie liniowe w jednej osi. Dla mojego przypadku musiałbym ich zastosować co najmniej 9 żeby określić położenie i orientację badanego obiektu, bo po 3 czujniki (1 na oś) na każdy umieszczony element śledzony. Nie wiem, czy taka konfiguracja ma sens ( zakłócenia, wymiary produkowanych czujników), na razie też dopiero szukam informacji.
W labolatoriach stosuje się też oświetlacze IR i kamery z filtrem. Na badanym przedmiocie jest odrpomiennik (zwykle piłka od pink ponga). Potem analizuje obraz w prosty sposób i ma się położenie przedmiotu obserwowanego. Można też próbować używać OpenCV i badać położenie wzorca przyczepionego do badanego przedmiotu.
Kolega robił już takie testy i nawet fajnie to działało ( prosta analiza obrazu i poszukiwanie charakterystycznych punktów), ale tym razem mamy bardziej skomplikowane zadanie, bo śledzimy punkty osadzone wewnątrz jamy ustnej i to ogranicza nas praktycznie chyba tylko do czujników inercyjnych.
Witam. Czy jest w stanie ktoś wspomóc wiedzą? Zrobiłem wszystko tak jak w tych instrukcjach krok po kroku, gdyż zaczynam dopiero swoją przygode z arduino, jednak cały czas akcelerometr wysyła mi jedną cały czas taką samą wartość mimo że poruszam nim na każdy możliwy sposób itp, jednak cały czas mam jedną wartośc. Co może być źle?
Masz taki sam typ akcelerometru?
Dokładnie taki sam typ akcelerometru. i działa to z tym błędem nawet, bo gdy CS nie jest podłaczony do Vcc to wyświetla Error a gdy jest podłączony otrzymuje wartość jakąś, ale cały czas taką samą bez względu na to jak poruszam akcelerometrem
Witam, mam jedno pytanie w jaki sposób przerobić powyższy kod żeby akcelerometr łączył się za pomocą magistrali SPI?
Proszę nie pisać o fizyce, jeśli nie ma się o niej pojęcia. Błędy: II zasady dynamiki nie opisuje zmian prędkości, nie ma czegoś takiego jak ujemne przyśpieszenie, g to przyśpieszenie ziemskie a nie siła grawitacji, na orbicie (jakiej?!?) siła grawitacji to jakieś 90 % tej na powierzchni Ziemi (to dla wysokości około 400 km), silnik samochodu pokonuje prawie wyłącznie siłę oporu aerodynamicznego a nie siłę tarcia, akcelerometr nie mierzy sił. I wreszcie to: „Jeśli zadziałasz na czujnik przyspieszeniem o przeciwnym kierunku niż został skierowany czujnik, to on zwróci nam wartość przyspieszenia jako ujemną.” No niekoniecznie. Załóżmy, że oś Z jest zwrócona w dół i akcelerometr leży na stole. Po normalizacji oczekuję wskazania 1g. Teraz „zadziałam na czujnik przyśpieszeniem” a = 3 m/s^2 zwróconym przeciwnie do osi Z. Akcelerometr zwróci wartość DODATNIĄ i równą 0,7 g.
Może się czepiam, ale fizyka to nauka ściśła i jeśli o niej pisać, to wypada ŚCIŚLE. Albo WCALE.